本文共 1499 字，大约阅读时间需要 4 分钟。

$$Idiot的乘幂$$

题目链接：

题目大意

已知$a$，$b$，$c$，$d$，$p$。

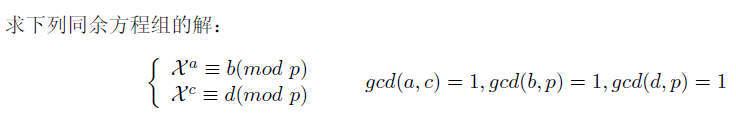
样例输入

1022 1 3 17 246 12 5 6 1316 16 9 1 1911 1 14 2 238 4 17 15 1910 3 9 1 1311 1 2 2 2313 2 14 12 1711 9 7 11 1415 10 7 7 17

样例输出

17251614318No Solution!1112

数据范围

思路

这道题是一道数学题。

（一脸懵逼的我只知道怎么做，不知道为什么） 斐蜀定理$ax+by=1$然后求$x$和$y$，然后就得出：$X\equiv X$^ax+cy$\equiv b^x{c}^y$ 然后用扩欧一波神奇操作可以求出$x$和$y$。（不要问我为什么，我推不出来） 如果$x$或者$y$是负数，要用逆元把它转成正数（因为我们要快速幂） 然后根据上面的式子$X\equiv b^x{c}^y$，把$x$和$y$带进去，就可以求出$X$。 不过要带进去验证一下（题目的方程），如果都成立就是答案，否则没有答案。

代码

#include
   
    #define ll long longusing namespace std;ll t, a, b, c, d, p, x, y;ll kuoou(ll a, ll b, ll &x, ll &y) {   //扩欧	if (b == 0) {   		x = 1;		y = 0;		return a;	}	ll answ = kuoou(b, a % b, y, x);	y -= a / b * x;	return answ;}ll ksm(ll a, ll b, ll p) {   //快速幂	ll an = 1;	while (b) {   		if (b & 1)			an = (an * a + p) % p;		a = (a * a + p) % p;		b >>= 1;	}	return an;}int main() {   	scanf("%lld", &t);//读入		for (ll i = 1; i <= t; i++) {   		scanf("%lld %lld %lld %lld %lld", &a, &b, &c, &d, &p);//读入		ll bb = b, dd = d, temp = 0;//初始化		kuoou(a, c, x, y);//求出		if (x < 0) {   //x为负数			kuoou(b, p, bb, temp);			x = -x;		}		if (y < 0) {   //y为负数			kuoou(d, p, dd, temp);			y = -y;		}		ll ans = ksm((bb % p + p) % p, x, p) * ksm((dd % p + p) % p, y, p) % p;//求出答案X		if ((ksm(ans, a, p) == b % p) && (ksm(ans, c, p) == d % p))//验证			printf("%lld\n", ans);//有答案		else printf("No Solution!\n");//没有答案	}		return 0; }
   

转载地址：http://doph.baihongyu.com/